硬核推导E=mc2的由来 张朝阳的物理课线下开讲

时间和空间不是各自独立的吗？怎么搅和到一块儿了？世界上最著名的方程E=mc2是怎么来的？3月11日，《张朝阳的物理课》线下“新春第一课”首次开讲，搜狐创始人、董事局主席兼CEO张朝阳与来自北京各高校的物理学子及物理爱好者们一起探讨物理的奥秘。

课堂上，他从光速不变理论出发，通过各种思想实验推导出时间膨胀、长度收缩、质速关系等违反直觉的相对论效应，利用质速关系与能量的定义进一步推导质能关系,并讲解了质能关系的意义与应用。之后又与现场同学讨论了此前直播课的相关问题，如薛定谔如何猜出薛定谔方程，如何用不确定性原理估算氢原子半径等。此外，人大附中物理教师、科普视频创作者李永乐也作为嘉宾现身课堂，与大家进行了互动交流。

第一堂线下物理课讨论“相对论” 直播风格独特强调“硬核推导”

“这个活动是非常独特的。”张朝阳在开场说道，“物理课我在线上已经完成三十讲了，覆盖了很多话题，今天别开生面，第一次走到线下。”

线下“新春第一课”，张朝阳重点讲解了狭义相对论中最著名的方程E=mc2，并结合案例加以解释。这个小小的公式蕴藏了巨大的能量，可以把一丁点儿的质量放大成巨大的能量，甚至原子弹、氢弹、太阳的能量都与此有关。张朝阳表示，“所以这个公式非常重要，与每个人的生活息息相关。”

“我的课比较强调硬核推导。”张朝阳介绍，要理解狭义相对论，必须先了解光速的特殊性。他先从麦克斯韦方程组导出的电磁波方程入手，指出光速与参考系无关这一反直觉的论述。他从光速不变出发，推导出时间膨胀效应，即运动的时钟相对于静止的时钟流逝较慢，说明此时时间与空间不再独立。

张朝阳解释，描述时间与空间的关系的方程就是洛伦兹变换，洛伦兹变换能把一个惯性参考系的坐标变换到另一个与之相对匀速运动的惯性参考系下。他在黑板上通过洛伦兹变换公式，结合“同时性的相对性”的概念推导出了“动尺缩短”公式，即运动的尺子在静止参考系下看，会比在尺子的固有参考系下短。

洛伦兹变换只是坐标的变换。张朝阳通过洛伦兹变换进一步导出了速度的变换公式，这与传统牛顿力学中简单的速度矢量的直接叠加有很大的不同。有了速度变换公式，他开始推导不同参考系下两个质量相同的小球的碰撞过程，结合动量守恒定律，并类比牛顿力学中动量的定义，计算出了“动质量”与速度的关系。

随后将力对位移进行积分，得出爱因斯坦最著名的质能方程E=mc2，它描述能量与质量的关系。张朝阳又以铀235的裂变过程为例，说明质量可以转化成能量，而其能量可以用爱因斯坦质能方程计算出来。

与同学现场对话讨论薛定谔方程 用量子力学公式推导氢原子半径

在其后的互动环节中，张朝阳还与同学们探讨了各种物理问题。包括薛定谔是如何猜测出薛定谔方程的？张朝阳对此进行了现场推导：爱因斯坦假设光子存在，并且提出了光的波粒二象性；德布罗意进一步假设所有物质都具有波粒二象性，且对于物质粒子，可以仿照电磁波的形式描写物质波；之后，波对时间求导可以得到能量相关的项，波对空间求导可以得到动量相关的项目；最后，将哈密顿量中的能量与动量换成相应的算符，并把研究对象用波函数形式表达，即可猜出薛定谔方程。

此外，对于“如何用不确定性原理估算出氢原子半径？”的问题，张朝阳解释，从经典电动力学的观点看，电子绕原子核转动会向外辐射电磁波，能量降低，且迅速塌缩到原子核里，那么氢原子就不能稳定存在了。但在量子力学中，定性地讲，动量与位置满足不确定性关系，电子往原子核塌缩时，其位置不确定度越小，动量不确定度就越大，从而让电子有远离原子核的趋势，抵消了电子往原子核塌缩的趋势。

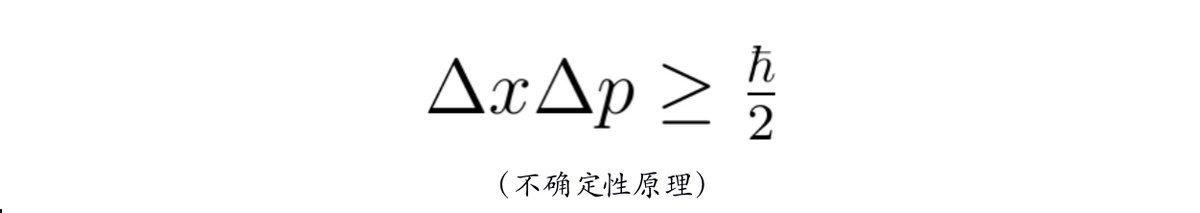
张朝阳不仅做了定性的说明，还做了定量的计算。他现场推导利用不确定性原理将动量表示成位置的不确定度并代入到哈密顿量中，计算出能量取最小值时的位置不确定度。这正是玻尔半径，也就是氢原子处于基态时电子的“轨道半径”，电子并不会塌缩到原子核内。张朝阳惊叹这种简单估算得到的结果竟然与严格求解薛定谔方程的结果相一致。这正体现了不确定性原理的简洁、深刻、有效。

上一篇：湖南省7所高校虚拟教研室入选教育部首批建设试
下一篇：没有了